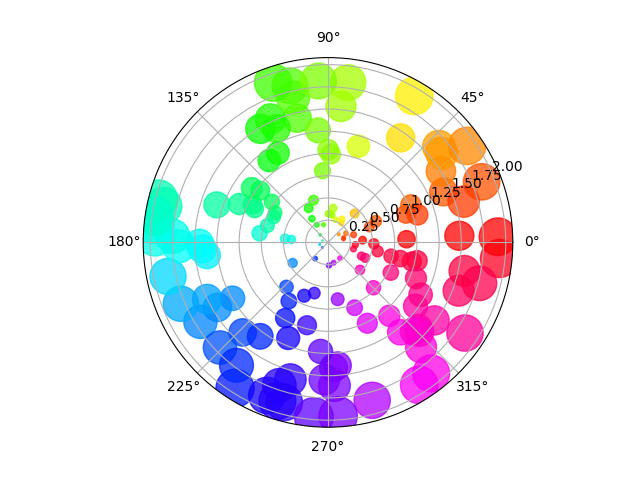
Streudiagramm auf der Polarachse #

Die Größe nimmt in diesem Beispiel radial zu und die Farbe nimmt mit dem Winkel zu (nur um zu überprüfen, ob die Symbole korrekt gestreut werden).

import numpy as np
import matplotlib.pyplot as plt


# Fixing random state for reproducibility
np.random.seed(19680801)

# Compute areas and colors
N = 150
r = 2 * np.random.rand(N)
theta = 2 * np.pi * np.random.rand(N)
area = 200 * r**2
colors = theta

fig = plt.figure()
ax = fig.add_subplot(projection='polar')
c = ax.scatter(theta, r, c=colors, s=area, cmap='hsv', alpha=0.75)

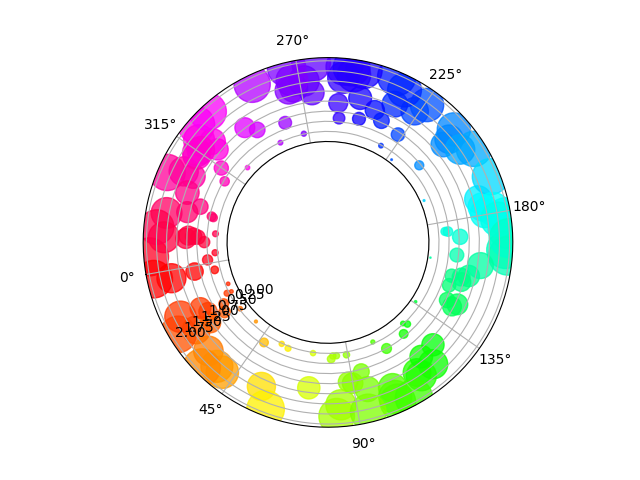
Streudiagramm auf Polarachse, mit versetztem Ursprung #

Der Hauptunterschied zum vorherigen Diagramm besteht in der Konfiguration des Ursprungsradius, wodurch ein Kreisring entsteht. Zusätzlich wird die Theta-Null-Position eingestellt, um die Darstellung zu drehen.

fig = plt.figure()
ax = fig.add_subplot(projection='polar')
c = ax.scatter(theta, r, c=colors, s=area, cmap='hsv', alpha=0.75)

ax.set_rorigin(-2.5)
ax.set_theta_zero_location('W', offset=10)

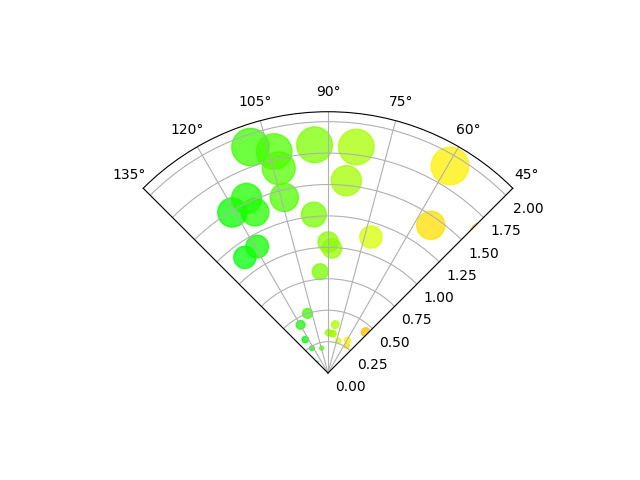
Streudiagramm auf der Polarachse, beschränkt auf einen Sektor #

Der Hauptunterschied zu den vorherigen Diagrammen besteht in der Konfiguration der Theta-Start- und -Endgrenzen, wodurch ein Sektor anstelle eines vollständigen Kreises entsteht.

fig = plt.figure()
ax = fig.add_subplot(projection='polar')
c = ax.scatter(theta, r, c=colors, s=area, cmap='hsv', alpha=0.75)

ax.set_thetamin(45)
ax.set_thetamax(135)

plt.show()

Verweise

In diesem Beispiel wird die Verwendung der folgenden Funktionen, Methoden, Klassen und Module gezeigt:

Gesamtlaufzeit des Skripts: ( 0 Minuten 1.739 Sekunden)

Galerie generiert von Sphinx-Gallery