Asinh-Demo

Darstellung der asinhAchsenskalierung, die die Transformation verwendet

\[a \rightarrow a_0 \sinh^{-1} (a / a_0)\]

Für Koordinatenwerte nahe Null (d. h. viel kleiner als die "lineare Breite")\(a_0\)), dies lässt die Werte im Wesentlichen unverändert:

\[a \rightarrow a + \mathcal{O}(a^3)\]

aber für größere Werte (zB\(|a| \gg a_0\), das ist asymptotisch

\[a \rightarrow a_0 \, \mathrm{sgn}(a) \ln |a| + \mathcal{O}(1)\]

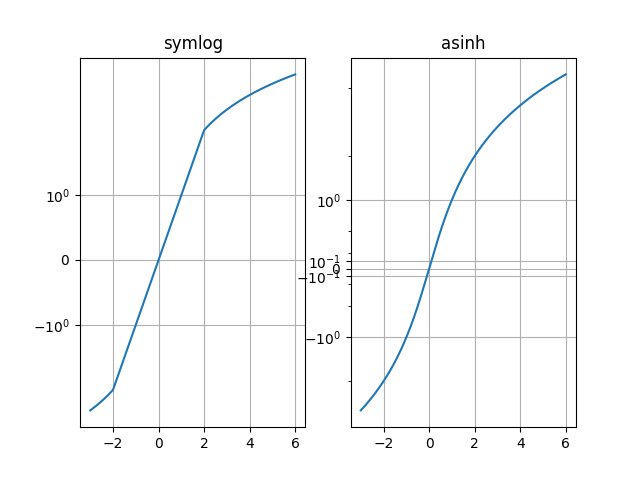
Wie bei der symlogSkalierung ermöglicht dies die Darstellung von Größen, die einen sehr großen dynamischen Bereich abdecken, der sowohl positive als auch negative Werte umfasst. Beinhaltet jedoch symlogeine Transformation, die Diskontinuitäten in ihrem Gradienten aufweist, da sie aus getrennten linearen und logarithmischen Transformationen aufgebaut ist. Die asinhSkalierung verwendet eine Transformation, die für alle (endlichen) Werte glatt ist, was sowohl mathematisch sauberer ist als auch visuelle Artefakte reduziert, die mit einem abrupten Übergang zwischen linearen und logarithmischen Bereichen des Diagramms verbunden sind.

Notiz

scale.AsinhScaleist experimentell und die API kann sich ändern.

Siehe . AsinhScale_SymmetricalLogScale

import numpy as np
import matplotlib.pyplot as plt

# Prepare sample values for variations on y=x graph:
x = np.linspace(-3, 6, 500)

Vergleichen Sie das Verhalten von "symlog" und "asinh" in einem y=x-Beispieldiagramm, in dem es einen diskontinuierlichen Gradienten in "symlog" in der Nähe von y=2 gibt:

fig1 = plt.figure()
ax0, ax1 = fig1.subplots(1, 2, sharex=True)

ax0.plot(x, x)
ax0.set_yscale('symlog')
ax0.grid()
ax0.set_title('symlog')

ax1.plot(x, x)
ax1.set_yscale('asinh')
ax1.grid()
ax1.set_title('asinh')

Text(0.5, 1.0, 'asinh')

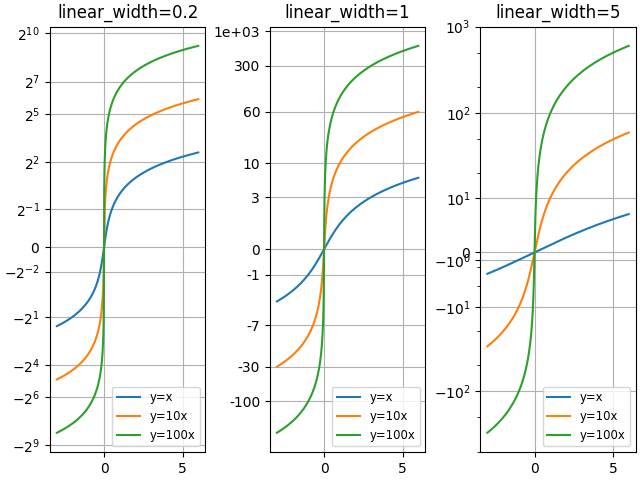
Vergleichen Sie "asinh"-Diagramme mit unterschiedlichem Skalierungsparameter "linear_width":

fig2 = plt.figure(constrained_layout=True)
axs = fig2.subplots(1, 3, sharex=True)
for ax, (a0, base) in zip(axs, ((0.2, 2), (1.0, 0), (5.0, 10))):
    ax.set_title('linear_width={:.3g}'.format(a0))
    ax.plot(x, x, label='y=x')
    ax.plot(x, 10*x, label='y=10x')
    ax.plot(x, 100*x, label='y=100x')
    ax.set_yscale('asinh', linear_width=a0, base=base)
    ax.grid()
    ax.legend(loc='best', fontsize='small')

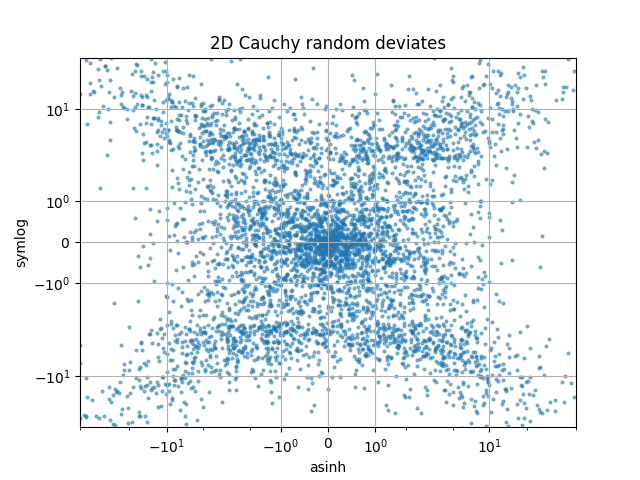
Vergleichen Sie die Skalierungen "symlog" und "asinh" bei 2D-Cauchy-verteilten Zufallszahlen, bei denen aufgrund der Gradientendiskontinuität in "symlog" möglicherweise subtilere Artefakte in der Nähe von y = 2 zu sehen sind:

fig3 = plt.figure()
ax = fig3.subplots(1, 1)
r = 3 * np.tan(np.random.uniform(-np.pi / 2.02, np.pi / 2.02,
                                 size=(5000,)))
th = np.random.uniform(0, 2*np.pi, size=r.shape)

ax.scatter(r * np.cos(th), r * np.sin(th), s=4, alpha=0.5)
ax.set_xscale('asinh')
ax.set_yscale('symlog')
ax.set_xlabel('asinh')
ax.set_ylabel('symlog')
ax.set_title('2D Cauchy random deviates')
ax.set_xlim(-50, 50)
ax.set_ylim(-50, 50)
ax.grid()

plt.show()

Verweise

• matplotlib.scale.AsinhScale

• matplotlib.ticker.AsinhLocator

• matplotlib.scale.SymmetricalLogScale