Füllen Sie zwischen und Alpha

Die fill_betweenFunktion generiert einen schattierten Bereich zwischen einer Mindest- und Höchstgrenze, der zur Veranschaulichung von Bereichen nützlich ist. Es hat ein sehr praktisches whereArgument, das Füllen mit logischen Bereichen zu kombinieren, z. B. um einfach eine Kurve über einem bestimmten Schwellenwert auszufüllen.

Auf der grundlegendsten Ebene fill_betweenkann es verwendet werden, um das visuelle Erscheinungsbild eines Diagramms zu verbessern. Vergleichen wir zwei Diagramme mit Finanzdaten mit einem einfachen Liniendiagramm auf der linken Seite und einer gefüllten Linie auf der rechten Seite.

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.cbook as cbook


# load up some sample financial data
r = (cbook.get_sample_data('goog.npz', np_load=True)['price_data']
     .view(np.recarray))
# create two subplots with the shared x and y axes
fig, (ax1, ax2) = plt.subplots(1, 2, sharex=True, sharey=True)

pricemin = r.close.min()

ax1.plot(r.date, r.close, lw=2)
ax2.fill_between(r.date, pricemin, r.close, alpha=0.7)

for ax in ax1, ax2:
    ax.grid(True)
    ax.label_outer()

ax1.set_ylabel('price')

fig.suptitle('Google (GOOG) daily closing price')
fig.autofmt_xdate()

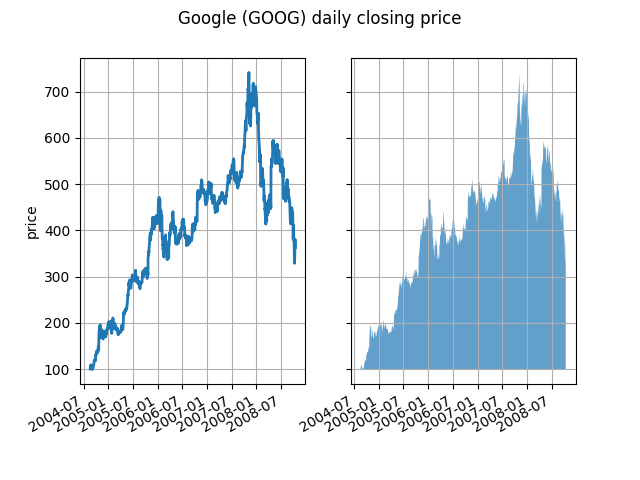
Der Alphakanal ist hier nicht erforderlich, kann aber verwendet werden, um Farben für optisch ansprechendere Plots weicher zu machen. In anderen Beispielen, wie wir unten sehen werden, ist der Alpha-Kanal funktional nützlich, da sich die schattierten Bereiche überlappen können und Alpha es Ihnen ermöglicht, beide zu sehen. Beachten Sie, dass das Postscript-Format kein Alpha unterstützt (dies ist eine Postscript-Beschränkung, keine Matplotlib-Beschränkung). Wenn Sie also Alpha verwenden, speichern Sie Ihre Figuren in PNG, PDF oder SVG.

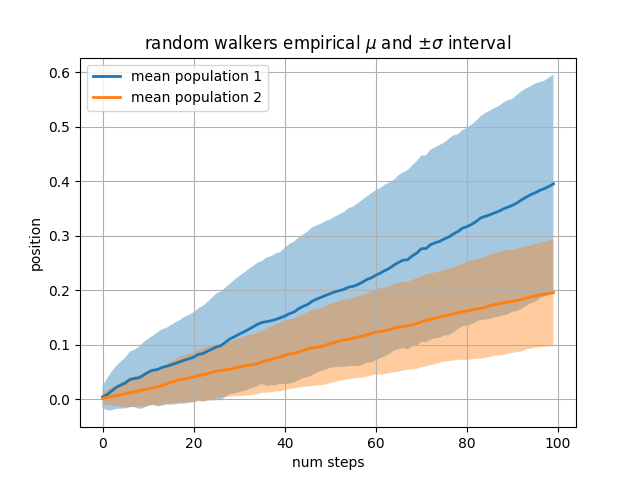
Unser nächstes Beispiel berechnet zwei Populationen von Random Walkern mit unterschiedlichem Mittelwert und unterschiedlicher Standardabweichung der Normalverteilungen, aus denen die Schritte gezogen werden. Wir verwenden gefüllte Regionen, um +/- eine Standardabweichung der mittleren Position der Population darzustellen. Hier ist der Alphakanal nützlich, nicht nur ästhetisch.

# Fixing random state for reproducibility
np.random.seed(19680801)

Nsteps, Nwalkers = 100, 250
t = np.arange(Nsteps)

# an (Nsteps x Nwalkers) array of random walk steps
S1 = 0.004 + 0.02*np.random.randn(Nsteps, Nwalkers)
S2 = 0.002 + 0.01*np.random.randn(Nsteps, Nwalkers)

# an (Nsteps x Nwalkers) array of random walker positions
X1 = S1.cumsum(axis=0)
X2 = S2.cumsum(axis=0)


# Nsteps length arrays empirical means and standard deviations of both
# populations over time
mu1 = X1.mean(axis=1)
sigma1 = X1.std(axis=1)
mu2 = X2.mean(axis=1)
sigma2 = X2.std(axis=1)

# plot it!
fig, ax = plt.subplots(1)
ax.plot(t, mu1, lw=2, label='mean population 1')
ax.plot(t, mu2, lw=2, label='mean population 2')
ax.fill_between(t, mu1+sigma1, mu1-sigma1, facecolor='C0', alpha=0.4)
ax.fill_between(t, mu2+sigma2, mu2-sigma2, facecolor='C1', alpha=0.4)
ax.set_title(r'random walkers empirical $\mu$ and $\pm \sigma$ interval')
ax.legend(loc='upper left')
ax.set_xlabel('num steps')
ax.set_ylabel('position')
ax.grid()

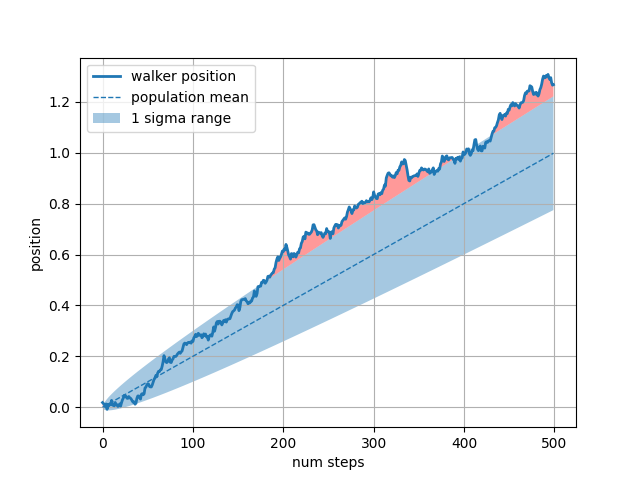
Das whereSchlüsselwortargument ist sehr praktisch, um bestimmte Bereiche des Diagramms hervorzuheben. wherenimmt eine boolesche Maske mit der gleichen Länge wie die x-, ymin- und ymax-Argumente und füllt nur den Bereich aus, in dem die boolesche Maske wahr ist. Im folgenden Beispiel simulieren wir einen einzelnen Random Walker und berechnen den analytischen Mittelwert und die Standardabweichung der Populationspositionen. Der Mittelwert der Grundgesamtheit ist als gestrichelte Linie dargestellt, und die plus/minus ein Sigma-Abweichung vom Mittelwert ist als ausgefüllter Bereich dargestellt. Wir verwenden die Where-Maske , um die Region zu finden, in der sich der Wanderer außerhalb der Ein-Sigma-Grenze befindet, und schattieren diese Region rot.X > upper_bound

# Fixing random state for reproducibility
np.random.seed(1)

Nsteps = 500
t = np.arange(Nsteps)

mu = 0.002
sigma = 0.01

# the steps and position
S = mu + sigma*np.random.randn(Nsteps)
X = S.cumsum()

# the 1 sigma upper and lower analytic population bounds
lower_bound = mu*t - sigma*np.sqrt(t)
upper_bound = mu*t + sigma*np.sqrt(t)

fig, ax = plt.subplots(1)
ax.plot(t, X, lw=2, label='walker position')
ax.plot(t, mu*t, lw=1, label='population mean', color='C0', ls='--')
ax.fill_between(t, lower_bound, upper_bound, facecolor='C0', alpha=0.4,
                label='1 sigma range')
ax.legend(loc='upper left')

# here we use the where argument to only fill the region where the
# walker is above the population 1 sigma boundary
ax.fill_between(t, upper_bound, X, where=X > upper_bound, fc='red', alpha=0.4)
ax.fill_between(t, lower_bound, X, where=X < lower_bound, fc='red', alpha=0.4)
ax.set_xlabel('num steps')
ax.set_ylabel('position')
ax.grid()

Eine weitere praktische Verwendung gefüllter Regionen ist das Hervorheben horizontaler oder vertikaler Spannen einer Achse - dafür hat Matplotlib die Hilfsfunktionen axhspanund axvspan. Siehe axhspan-Demo .

plt.show()