Notiz
Klicken Sie hier , um den vollständigen Beispielcode herunterzuladen
Plots kommentieren #
Die folgenden Beispiele zeigen, wie es möglich ist, Diagramme in Matplotlib zu kommentieren. Dazu gehören das Hervorheben bestimmter interessanter Punkte und der Einsatz verschiedener visueller Tools, um die Aufmerksamkeit auf diesen Punkt zu lenken. Eine vollständigere und ausführlichere Beschreibung der Anmerkungs- und Textwerkzeuge in Matplotlib finden Sie im Tutorial zu Anmerkungen .
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
import numpy as np
from matplotlib.text import OffsetFrom
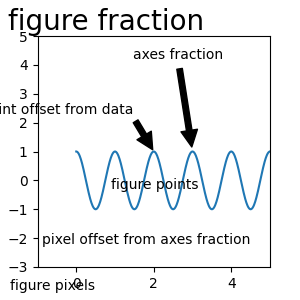
Festlegen von Textpunkten und Anmerkungspunkten #
Sie müssen einen Anmerkungspunkt angeben , um diesen Punkt zu kommentieren. Zusätzlich können Sie einen Textpunkt für die Position des Textes für diese Anmerkung angeben. Optional können Sie das Koordinatensystem von xy und xytext mit einem der folgenden Strings für xycoords
und textcoords angeben (Standard ist 'data'):xy=(x, y)xytext=(x, y)
'figure points' : points from the lower left corner of the figure
'figure pixels' : pixels from the lower left corner of the figure
'figure fraction' : (0, 0) is lower left of figure and (1, 1) is upper right
'axes points' : points from lower left corner of axes
'axes pixels' : pixels from lower left corner of axes
'axes fraction' : (0, 0) is lower left of axes and (1, 1) is upper right
'offset points' : Specify an offset (in points) from the xy value
'offset pixels' : Specify an offset (in pixels) from the xy value
'data' : use the axes data coordinate system
Hinweis: Bei physikalischen Koordinatensystemen (Punkte oder Pixel) ist der Ursprung (unten, links) der Figur oder Achsen.
Optional können Sie Pfeileigenschaften angeben, die einen Pfeil vom Text zum annotierten Punkt zeichnen, indem Sie ein Wörterbuch mit Pfeileigenschaften angeben
Gültige Schlüssel sind:
width : the width of the arrow in points
frac : the fraction of the arrow length occupied by the head
headwidth : the width of the base of the arrow head in points
shrink : move the tip and base some percent away from the
annotated point and text
any key for matplotlib.patches.polygon (e.g., facecolor)
# Create our figure and data we'll use for plotting
fig, ax = plt.subplots(figsize=(3, 3))
t = np.arange(0.0, 5.0, 0.01)
s = np.cos(2*np.pi*t)
# Plot a line and add some simple annotations
line, = ax.plot(t, s)
ax.annotate('figure pixels',
xy=(10, 10), xycoords='figure pixels')
ax.annotate('figure points',
xy=(80, 80), xycoords='figure points')
ax.annotate('figure fraction',
xy=(.025, .975), xycoords='figure fraction',
horizontalalignment='left', verticalalignment='top',
fontsize=20)
# The following examples show off how these arrows are drawn.
ax.annotate('point offset from data',
xy=(2, 1), xycoords='data',
xytext=(-15, 25), textcoords='offset points',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='right', verticalalignment='bottom')
ax.annotate('axes fraction',
xy=(3, 1), xycoords='data',
xytext=(0.8, 0.95), textcoords='axes fraction',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='right', verticalalignment='top')
# You may also use negative points or pixels to specify from (right, top).
# E.g., (-10, 10) is 10 points to the left of the right side of the axes and 10
# points above the bottom
ax.annotate('pixel offset from axes fraction',
xy=(1, 0), xycoords='axes fraction',
xytext=(-20, 20), textcoords='offset pixels',
horizontalalignment='right',
verticalalignment='bottom')
ax.set(xlim=(-1, 5), ylim=(-3, 5))
[(-1.0, 5.0), (-3.0, 5.0)]
Mehrere Koordinatensysteme und Achsentypen verwenden #
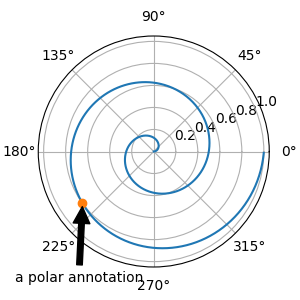
Sie können den XY-Punkt und den XY-Text in verschiedenen Positionen und Koordinatensystemen angeben , optional eine Verbindungslinie einschalten und den Punkt mit einem Marker markieren. Anmerkungen funktionieren auch auf Polarachsen.
Im folgenden Beispiel befindet sich der xy -Punkt in nativen Koordinaten ( xycoords ist standardmäßig „data“). Bei Polarachsen liegt dies im (Theta-, Radius-) Raum. Der Text im Beispiel wird im Koordinatensystem für Bruchzahlen platziert. Textschlüsselwortargumente wie horizontale und vertikale Ausrichtung werden berücksichtigt.
fig, ax = plt.subplots(subplot_kw=dict(projection='polar'), figsize=(3, 3))
r = np.arange(0, 1, 0.001)
theta = 2*2*np.pi*r
line, = ax.plot(theta, r)
ind = 800
thisr, thistheta = r[ind], theta[ind]
ax.plot([thistheta], [thisr], 'o')
ax.annotate('a polar annotation',
xy=(thistheta, thisr), # theta, radius
xytext=(0.05, 0.05), # fraction, fraction
textcoords='figure fraction',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='left',
verticalalignment='bottom')
Text(0.05, 0.05, 'a polar annotation')
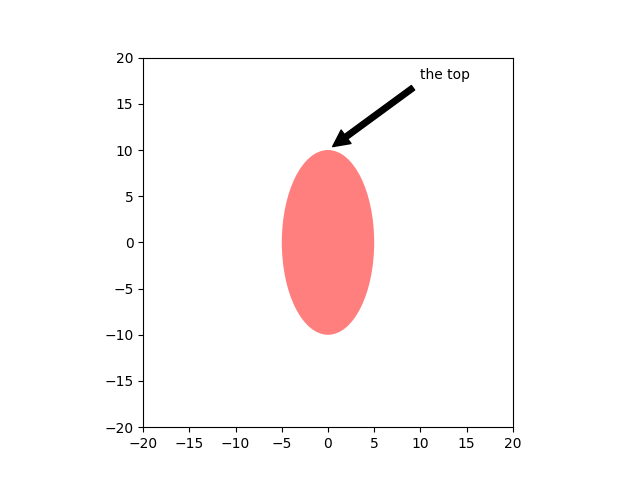
Sie können auch die Polarnotation auf kartesischen Achsen verwenden. Hier ist das native Koordinatensystem ('data') kartesisch, daher müssen Sie die xycoords und textcoords als 'polar' angeben, wenn Sie (theta, radius) verwenden möchten.
el = Ellipse((0, 0), 10, 20, facecolor='r', alpha=0.5)
fig, ax = plt.subplots(subplot_kw=dict(aspect='equal'))
ax.add_artist(el)
el.set_clip_box(ax.bbox)
ax.annotate('the top',
xy=(np.pi/2., 10.), # theta, radius
xytext=(np.pi/3, 20.), # theta, radius
xycoords='polar',
textcoords='polar',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='left',
verticalalignment='bottom',
clip_on=True) # clip to the axes bounding box
ax.set(xlim=[-20, 20], ylim=[-20, 20])
[(-20.0, 20.0), (-20.0, 20.0)]
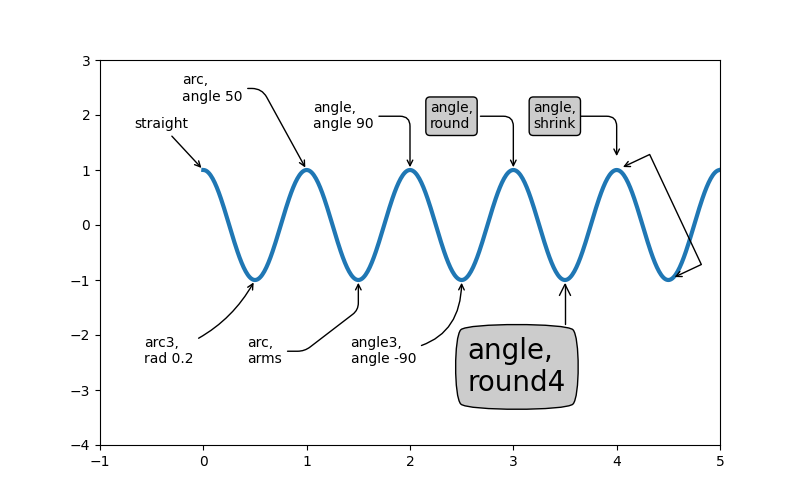
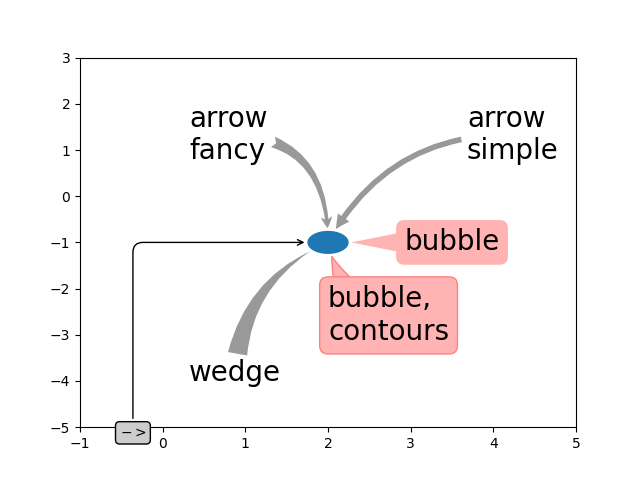
Anpassen von Pfeil- und Blasenstilen #
Der Pfeil zwischen xytext und dem Anmerkungspunkt sowie die Sprechblase, die den Anmerkungstext bedeckt, sind in hohem Maße anpassbar. Nachfolgend finden Sie einige Parameteroptionen sowie deren resultierende Ausgabe.
fig, ax = plt.subplots(figsize=(8, 5))
t = np.arange(0.0, 5.0, 0.01)
s = np.cos(2*np.pi*t)
line, = ax.plot(t, s, lw=3)
ax.annotate(
'straight',
xy=(0, 1), xycoords='data',
xytext=(-50, 30), textcoords='offset points',
arrowprops=dict(arrowstyle="->"))
ax.annotate(
'arc3,\nrad 0.2',
xy=(0.5, -1), xycoords='data',
xytext=(-80, -60), textcoords='offset points',
arrowprops=dict(arrowstyle="->",
connectionstyle="arc3,rad=.2"))
ax.annotate(
'arc,\nangle 50',
xy=(1., 1), xycoords='data',
xytext=(-90, 50), textcoords='offset points',
arrowprops=dict(arrowstyle="->",
connectionstyle="arc,angleA=0,armA=50,rad=10"))
ax.annotate(
'arc,\narms',
xy=(1.5, -1), xycoords='data',
xytext=(-80, -60), textcoords='offset points',
arrowprops=dict(
arrowstyle="->",
connectionstyle="arc,angleA=0,armA=40,angleB=-90,armB=30,rad=7"))
ax.annotate(
'angle,\nangle 90',
xy=(2., 1), xycoords='data',
xytext=(-70, 30), textcoords='offset points',
arrowprops=dict(arrowstyle="->",
connectionstyle="angle,angleA=0,angleB=90,rad=10"))
ax.annotate(
'angle3,\nangle -90',
xy=(2.5, -1), xycoords='data',
xytext=(-80, -60), textcoords='offset points',
arrowprops=dict(arrowstyle="->",
connectionstyle="angle3,angleA=0,angleB=-90"))
ax.annotate(
'angle,\nround',
xy=(3., 1), xycoords='data',
xytext=(-60, 30), textcoords='offset points',
bbox=dict(boxstyle="round", fc="0.8"),
arrowprops=dict(arrowstyle="->",
connectionstyle="angle,angleA=0,angleB=90,rad=10"))
ax.annotate(
'angle,\nround4',
xy=(3.5, -1), xycoords='data',
xytext=(-70, -80), textcoords='offset points',
size=20,
bbox=dict(boxstyle="round4,pad=.5", fc="0.8"),
arrowprops=dict(arrowstyle="->",
connectionstyle="angle,angleA=0,angleB=-90,rad=10"))
ax.annotate(
'angle,\nshrink',
xy=(4., 1), xycoords='data',
xytext=(-60, 30), textcoords='offset points',
bbox=dict(boxstyle="round", fc="0.8"),
arrowprops=dict(arrowstyle="->",
shrinkA=0, shrinkB=10,
connectionstyle="angle,angleA=0,angleB=90,rad=10"))
# You can pass an empty string to get only annotation arrows rendered
ax.annotate('', xy=(4., 1.), xycoords='data',
xytext=(4.5, -1), textcoords='data',
arrowprops=dict(arrowstyle="<->",
connectionstyle="bar",
ec="k",
shrinkA=5, shrinkB=5))
ax.set(xlim=(-1, 5), ylim=(-4, 3))
[(-1.0, 5.0), (-4.0, 3.0)]
Wir erstellen eine weitere Figur, damit es nicht zu unübersichtlich wird
fig, ax = plt.subplots()
el = Ellipse((2, -1), 0.5, 0.5)
ax.add_patch(el)
ax.annotate('$->$',
xy=(2., -1), xycoords='data',
xytext=(-150, -140), textcoords='offset points',
bbox=dict(boxstyle="round", fc="0.8"),
arrowprops=dict(arrowstyle="->",
patchB=el,
connectionstyle="angle,angleA=90,angleB=0,rad=10"))
ax.annotate('arrow\nfancy',
xy=(2., -1), xycoords='data',
xytext=(-100, 60), textcoords='offset points',
size=20,
arrowprops=dict(arrowstyle="fancy",
fc="0.6", ec="none",
patchB=el,
connectionstyle="angle3,angleA=0,angleB=-90"))
ax.annotate('arrow\nsimple',
xy=(2., -1), xycoords='data',
xytext=(100, 60), textcoords='offset points',
size=20,
arrowprops=dict(arrowstyle="simple",
fc="0.6", ec="none",
patchB=el,
connectionstyle="arc3,rad=0.3"))
ax.annotate('wedge',
xy=(2., -1), xycoords='data',
xytext=(-100, -100), textcoords='offset points',
size=20,
arrowprops=dict(arrowstyle="wedge,tail_width=0.7",
fc="0.6", ec="none",
patchB=el,
connectionstyle="arc3,rad=-0.3"))
ax.annotate('bubble,\ncontours',
xy=(2., -1), xycoords='data',
xytext=(0, -70), textcoords='offset points',
size=20,
bbox=dict(boxstyle="round",
fc=(1.0, 0.7, 0.7),
ec=(1., .5, .5)),
arrowprops=dict(arrowstyle="wedge,tail_width=1.",
fc=(1.0, 0.7, 0.7), ec=(1., .5, .5),
patchA=None,
patchB=el,
relpos=(0.2, 0.8),
connectionstyle="arc3,rad=-0.1"))
ax.annotate('bubble',
xy=(2., -1), xycoords='data',
xytext=(55, 0), textcoords='offset points',
size=20, va="center",
bbox=dict(boxstyle="round", fc=(1.0, 0.7, 0.7), ec="none"),
arrowprops=dict(arrowstyle="wedge,tail_width=1.",
fc=(1.0, 0.7, 0.7), ec="none",
patchA=None,
patchB=el,
relpos=(0.2, 0.5)))
ax.set(xlim=(-1, 5), ylim=(-5, 3))
[(-1.0, 5.0), (-5.0, 3.0)]
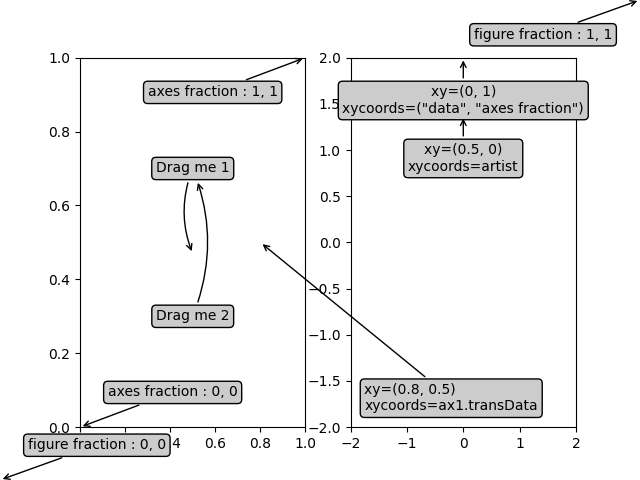
Weitere Beispiele für Koordinatensysteme #
Nachfolgend zeigen wir einige weitere Beispiele für Koordinatensysteme und wie die Position von Anmerkungen angegeben werden kann.
fig, (ax1, ax2) = plt.subplots(1, 2)
bbox_args = dict(boxstyle="round", fc="0.8")
arrow_args = dict(arrowstyle="->")
# Here we'll demonstrate the extents of the coordinate system and how
# we place annotating text.
ax1.annotate('figure fraction : 0, 0', xy=(0, 0), xycoords='figure fraction',
xytext=(20, 20), textcoords='offset points',
ha="left", va="bottom",
bbox=bbox_args,
arrowprops=arrow_args)
ax1.annotate('figure fraction : 1, 1', xy=(1, 1), xycoords='figure fraction',
xytext=(-20, -20), textcoords='offset points',
ha="right", va="top",
bbox=bbox_args,
arrowprops=arrow_args)
ax1.annotate('axes fraction : 0, 0', xy=(0, 0), xycoords='axes fraction',
xytext=(20, 20), textcoords='offset points',
ha="left", va="bottom",
bbox=bbox_args,
arrowprops=arrow_args)
ax1.annotate('axes fraction : 1, 1', xy=(1, 1), xycoords='axes fraction',
xytext=(-20, -20), textcoords='offset points',
ha="right", va="top",
bbox=bbox_args,
arrowprops=arrow_args)
# It is also possible to generate draggable annotations
an1 = ax1.annotate('Drag me 1', xy=(.5, .7), xycoords='data',
ha="center", va="center",
bbox=bbox_args)
an2 = ax1.annotate('Drag me 2', xy=(.5, .5), xycoords=an1,
xytext=(.5, .3), textcoords='axes fraction',
ha="center", va="center",
bbox=bbox_args,
arrowprops=dict(patchB=an1.get_bbox_patch(),
connectionstyle="arc3,rad=0.2",
**arrow_args))
an1.draggable()
an2.draggable()
an3 = ax1.annotate('', xy=(.5, .5), xycoords=an2,
xytext=(.5, .5), textcoords=an1,
ha="center", va="center",
bbox=bbox_args,
arrowprops=dict(patchA=an1.get_bbox_patch(),
patchB=an2.get_bbox_patch(),
connectionstyle="arc3,rad=0.2",
**arrow_args))
# Finally we'll show off some more complex annotation and placement
text = ax2.annotate('xy=(0, 1)\nxycoords=("data", "axes fraction")',
xy=(0, 1), xycoords=("data", 'axes fraction'),
xytext=(0, -20), textcoords='offset points',
ha="center", va="top",
bbox=bbox_args,
arrowprops=arrow_args)
ax2.annotate('xy=(0.5, 0)\nxycoords=artist',
xy=(0.5, 0.), xycoords=text,
xytext=(0, -20), textcoords='offset points',
ha="center", va="top",
bbox=bbox_args,
arrowprops=arrow_args)
ax2.annotate('xy=(0.8, 0.5)\nxycoords=ax1.transData',
xy=(0.8, 0.5), xycoords=ax1.transData,
xytext=(10, 10),
textcoords=OffsetFrom(ax2.bbox, (0, 0), "points"),
ha="left", va="bottom",
bbox=bbox_args,
arrowprops=arrow_args)
ax2.set(xlim=[-2, 2], ylim=[-2, 2])
plt.show()
Gesamtlaufzeit des Skripts: ( 0 Minuten 2.463 Sekunden)