Verwenden von Histogrammen zum Zeichnen einer kumulativen Verteilung

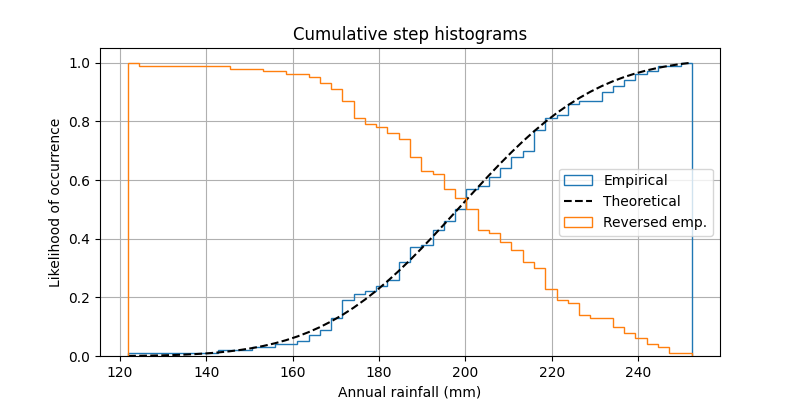
Dies zeigt, wie ein kumulatives, normalisiertes Histogramm als Stufenfunktion gezeichnet wird, um die empirische kumulative Verteilungsfunktion (CDF) einer Stichprobe zu visualisieren. Wir zeigen auch die theoretische CDF.

Ein paar andere Optionen für die histFunktion werden demonstriert. Wir verwenden nämlich den normierten Parameter, um das Histogramm zu normalisieren, und ein paar verschiedene Optionen für den kumulativen Parameter. Der normierte Parameter nimmt einen booleschen Wert an. Wenn True, werden die Klassenhöhen so skaliert, dass die Gesamtfläche des Histogramms 1 beträgt. Das kumulative Schlüsselwortargument ist etwas nuancierter. Wie normed können Sie True oder False übergeben, aber Sie können auch -1 übergeben, um die Verteilung umzukehren.

Da wir ein normalisiertes und kumulatives Histogramm zeigen, sind diese Kurven effektiv die kumulativen Verteilungsfunktionen (CDFs) der Stichproben. In der Technik werden empirische CDFs manchmal als "Nichtüberschreitungskurven" bezeichnet. Mit anderen Worten, Sie können den y-Wert für einen gegebenen x-Wert betrachten, um die Wahrscheinlichkeit und Beobachtung aus der Stichprobe zu erhalten, die diesen x-Wert nicht überschreitet. Beispielsweise entspricht der Wert von 225 auf der x-Achse etwa 0,85 auf der y-Achse, sodass eine Wahrscheinlichkeit von 85 % besteht, dass eine Beobachtung in der Stichprobe 225 nicht cumulativeüberschreitet die letzte Reihe für dieses Beispiel erzeugt eine "Überschreitungs"-Kurve.

Die Auswahl unterschiedlicher Bin-Anzahlen und -Größen kann die Form eines Histogramms erheblich beeinflussen. Die Astropy-Dokumentation enthält einen großartigen Abschnitt zur Auswahl dieser Parameter: http://docs.astropy.org/en/stable/visualization/histogram.html

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(19680801)

mu = 200
sigma = 25
n_bins = 50
x = np.random.normal(mu, sigma, size=100)

fig, ax = plt.subplots(figsize=(8, 4))

# plot the cumulative histogram
n, bins, patches = ax.hist(x, n_bins, density=True, histtype='step',
                           cumulative=True, label='Empirical')

# Add a line showing the expected distribution.
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
     np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
y = y.cumsum()
y /= y[-1]

ax.plot(bins, y, 'k--', linewidth=1.5, label='Theoretical')

# Overlay a reversed cumulative histogram.
ax.hist(x, bins=bins, density=True, histtype='step', cumulative=-1,
        label='Reversed emp.')

# tidy up the figure
ax.grid(True)
ax.legend(loc='right')
ax.set_title('Cumulative step histograms')
ax.set_xlabel('Annual rainfall (mm)')
ax.set_ylabel('Likelihood of occurrence')

plt.show()

Verweise

In diesem Beispiel wird die Verwendung der folgenden Funktionen, Methoden, Klassen und Module gezeigt:

• matplotlib.axes.Axes.hist/matplotlib.pyplot.hist