Zeichnen Sie eine Vertrauensellipse eines zweidimensionalen Datensatzes

Dieses Beispiel zeigt, wie eine Vertrauensellipse eines zweidimensionalen Datensatzes unter Verwendung seines Pearson-Korrelationskoeffizienten gezeichnet wird.

Der Ansatz, der verwendet wird, um die richtige Geometrie zu erhalten, wird hier erklärt und bewiesen:

https://carstenschelp.github.io/2018/09/14/Plot_Confidence_Ellipse_001.html

Das Verfahren vermeidet die Verwendung eines iterativen Eigenzerlegungsalgorithmus und nutzt die Tatsache, dass eine normalisierte Kovarianzmatrix (zusammengesetzt aus Pearson-Korrelationskoeffizienten und Einsen) besonders einfach zu handhaben ist.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
import matplotlib.transforms as transforms

Die Plotfunktion selbst

Diese Funktion zeichnet die Vertrauensellipse der Kovarianz der gegebenen Array-ähnlichen Variablen x und y. Die Ellipse wird in das gegebene Achsenobjekt ax eingezeichnet.

Die Radien der Ellipse können durch n_std gesteuert werden, was die Anzahl der Standardabweichungen ist. Der Standardwert ist 3, wodurch die Ellipse 98,9 % der Punkte umschließt, wenn die Daten wie in diesen Beispielen normal verteilt sind (3 Standardabweichungen in 1-D enthalten 99,7 % der Daten, was 98,9 % der Daten in 2-D entspricht). D).

def confidence_ellipse(x, y, ax, n_std=3.0, facecolor='none', **kwargs):
    """
    Create a plot of the covariance confidence ellipse of *x* and *y*.

    Parameters
    ----------
    x, y : array-like, shape (n, )
        Input data.

    ax : matplotlib.axes.Axes
        The axes object to draw the ellipse into.

    n_std : float
        The number of standard deviations to determine the ellipse's radiuses.

    **kwargs
        Forwarded to `~matplotlib.patches.Ellipse`

    Returns
    -------
    matplotlib.patches.Ellipse
    """
    if x.size != y.size:
        raise ValueError("x and y must be the same size")

    cov = np.cov(x, y)
    pearson = cov[0, 1]/np.sqrt(cov[0, 0] * cov[1, 1])
    # Using a special case to obtain the eigenvalues of this
    # two-dimensional dataset.
    ell_radius_x = np.sqrt(1 + pearson)
    ell_radius_y = np.sqrt(1 - pearson)
    ellipse = Ellipse((0, 0), width=ell_radius_x * 2, height=ell_radius_y * 2,
                      facecolor=facecolor, **kwargs)

    # Calculating the standard deviation of x from
    # the squareroot of the variance and multiplying
    # with the given number of standard deviations.
    scale_x = np.sqrt(cov[0, 0]) * n_std
    mean_x = np.mean(x)

    # calculating the standard deviation of y ...
    scale_y = np.sqrt(cov[1, 1]) * n_std
    mean_y = np.mean(y)

    transf = transforms.Affine2D() \
        .rotate_deg(45) \
        .scale(scale_x, scale_y) \
        .translate(mean_x, mean_y)

    ellipse.set_transform(transf + ax.transData)
    return ax.add_patch(ellipse)

Eine Hilfsfunktion zum Erstellen eines korrelierten Datensatzes

Erstellt einen zufälligen zweidimensionalen Datensatz mit dem angegebenen zweidimensionalen Mittelwert (mu) und den angegebenen Dimensionen (Skala). Die Korrelation kann über den Parameter 'dependency', eine 2x2-Matrix, gesteuert werden.

def get_correlated_dataset(n, dependency, mu, scale):
    latent = np.random.randn(n, 2)
    dependent = latent.dot(dependency)
    scaled = dependent * scale
    scaled_with_offset = scaled + mu
    # return x and y of the new, correlated dataset
    return scaled_with_offset[:, 0], scaled_with_offset[:, 1]

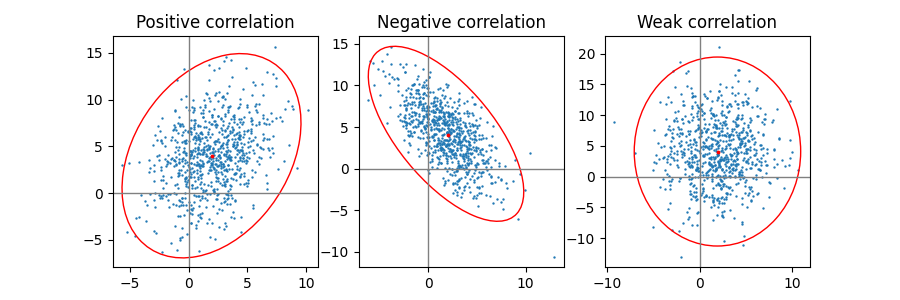
Positive, negative und schwache Korrelation

Beachten Sie, dass die Form für die schwache Korrelation (rechts) eine Ellipse und kein Kreis ist, da x und y unterschiedlich skaliert sind. Die Tatsache, dass x und y unkorreliert sind, wird jedoch dadurch angezeigt, dass die Achsen der Ellipse mit der x- und y-Achse des Koordinatensystems ausgerichtet sind.

np.random.seed(0)

PARAMETERS = {
    'Positive correlation': [[0.85, 0.35],
                             [0.15, -0.65]],
    'Negative correlation': [[0.9, -0.4],
                             [0.1, -0.6]],
    'Weak correlation': [[1, 0],
                         [0, 1]],
}

mu = 2, 4
scale = 3, 5

fig, axs = plt.subplots(1, 3, figsize=(9, 3))
for ax, (title, dependency) in zip(axs, PARAMETERS.items()):
    x, y = get_correlated_dataset(800, dependency, mu, scale)
    ax.scatter(x, y, s=0.5)

    ax.axvline(c='grey', lw=1)
    ax.axhline(c='grey', lw=1)

    confidence_ellipse(x, y, ax, edgecolor='red')

    ax.scatter(mu[0], mu[1], c='red', s=3)
    ax.set_title(title)

plt.show()

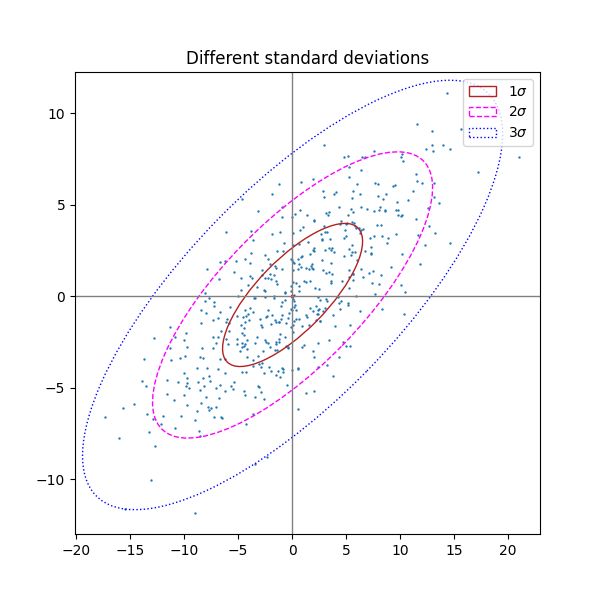
Unterschiedliche Anzahl von Standardabweichungen

Ein Diagramm mit n_std = 3 (blau), 2 (lila) und 1 (rot)

fig, ax_nstd = plt.subplots(figsize=(6, 6))

dependency_nstd = [[0.8, 0.75],
                   [-0.2, 0.35]]
mu = 0, 0
scale = 8, 5

ax_nstd.axvline(c='grey', lw=1)
ax_nstd.axhline(c='grey', lw=1)

x, y = get_correlated_dataset(500, dependency_nstd, mu, scale)
ax_nstd.scatter(x, y, s=0.5)

confidence_ellipse(x, y, ax_nstd, n_std=1,
                   label=r'$1\sigma$', edgecolor='firebrick')
confidence_ellipse(x, y, ax_nstd, n_std=2,
                   label=r'$2\sigma$', edgecolor='fuchsia', linestyle='--')
confidence_ellipse(x, y, ax_nstd, n_std=3,
                   label=r'$3\sigma$', edgecolor='blue', linestyle=':')

ax_nstd.scatter(mu[0], mu[1], c='red', s=3)
ax_nstd.set_title('Different standard deviations')
ax_nstd.legend()
plt.show()

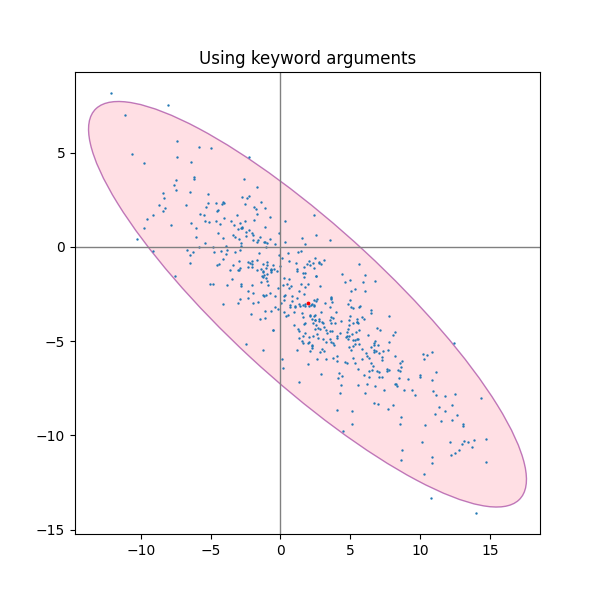
Verwenden der Schlüsselwortargumente

Verwenden Sie die für angegebenen Schlüsselwortargumente matplotlib.patches.Patch, um die Ellipse auf unterschiedliche Weise darzustellen.

fig, ax_kwargs = plt.subplots(figsize=(6, 6))
dependency_kwargs = [[-0.8, 0.5],
                     [-0.2, 0.5]]
mu = 2, -3
scale = 6, 5

ax_kwargs.axvline(c='grey', lw=1)
ax_kwargs.axhline(c='grey', lw=1)

x, y = get_correlated_dataset(500, dependency_kwargs, mu, scale)
# Plot the ellipse with zorder=0 in order to demonstrate
# its transparency (caused by the use of alpha).
confidence_ellipse(x, y, ax_kwargs,
                   alpha=0.5, facecolor='pink', edgecolor='purple', zorder=0)

ax_kwargs.scatter(x, y, s=0.5)
ax_kwargs.scatter(mu[0], mu[1], c='red', s=3)
ax_kwargs.set_title('Using keyword arguments')

fig.subplots_adjust(hspace=0.25)
plt.show()

Verweise

In diesem Beispiel wird die Verwendung der folgenden Funktionen, Methoden, Klassen und Module gezeigt:

• matplotlib.transforms.Affine2D

• matplotlib.patches.Ellipse