Konturieren des Lösungsraums von Optimierungen

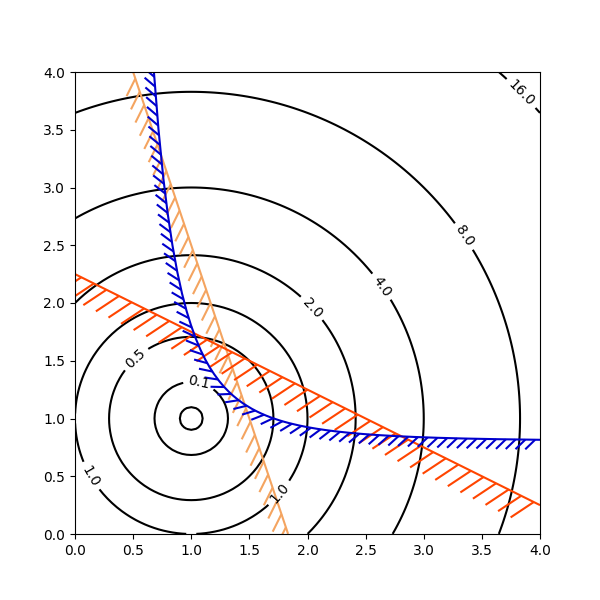
Das Plotten von Konturen ist besonders praktisch, um den Lösungsraum von Optimierungsproblemen zu veranschaulichen. Es kann nicht nur verwendet axes.Axes.contourwerden, um die Topographie der Zielfunktion darzustellen, es kann auch verwendet werden, um Grenzkurven der Beschränkungsfunktionen zu erzeugen. Die Beschränkungslinien können gezeichnet werden TickedStroke, um die gültigen und ungültigen Seiten der Beschränkungsgrenzen zu unterscheiden.

axes.Axes.contourerzeugt Kurven mit größeren Werten links von der Kontur. Der Winkelparameter wird null voraus mit zunehmenden Werten nach links gemessen. Folglich TickedStrokesollte der Winkel bei der Verwendung zur Veranschaulichung einer Beschränkung in einem typischen Optimierungsproblem zwischen null und 180 Grad eingestellt werden.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import patheffects

fig, ax = plt.subplots(figsize=(6, 6))

nx = 101
ny = 105

# Set up survey vectors
xvec = np.linspace(0.001, 4.0, nx)
yvec = np.linspace(0.001, 4.0, ny)

# Set up survey matrices.  Design disk loading and gear ratio.
x1, x2 = np.meshgrid(xvec, yvec)

# Evaluate some stuff to plot
obj = x1**2 + x2**2 - 2*x1 - 2*x2 + 2
g1 = -(3*x1 + x2 - 5.5)
g2 = -(x1 + 2*x2 - 4.5)
g3 = 0.8 + x1**-3 - x2

cntr = ax.contour(x1, x2, obj, [0.01, 0.1, 0.5, 1, 2, 4, 8, 16],
                  colors='black')
ax.clabel(cntr, fmt="%2.1f", use_clabeltext=True)

cg1 = ax.contour(x1, x2, g1, [0], colors='sandybrown')
plt.setp(cg1.collections,
         path_effects=[patheffects.withTickedStroke(angle=135)])

cg2 = ax.contour(x1, x2, g2, [0], colors='orangered')
plt.setp(cg2.collections,
         path_effects=[patheffects.withTickedStroke(angle=60, length=2)])

cg3 = ax.contour(x1, x2, g3, [0], colors='mediumblue')
plt.setp(cg3.collections,
         path_effects=[patheffects.withTickedStroke(spacing=7)])

ax.set_xlim(0, 4)
ax.set_ylim(0, 4)

plt.show()