Sekundärachse

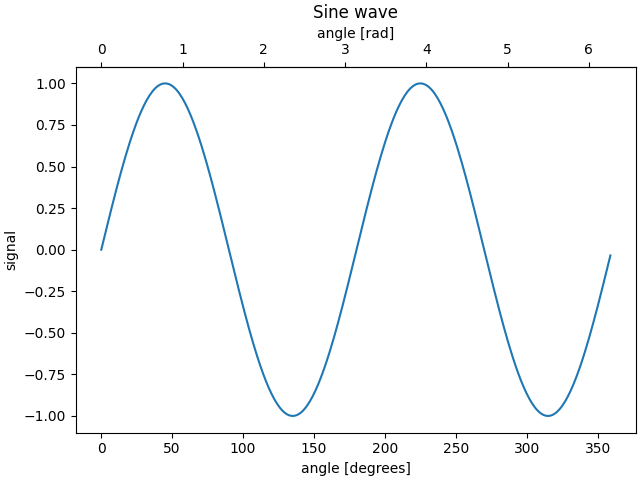
Manchmal möchten wir eine sekundäre Achse auf einem Diagramm, um beispielsweise Bogenmaß in Grad auf demselben Diagramm umzuwandeln. Wir können dies tun, indem wir eine untergeordnete Achse mit nur einer Achse über axes.Axes.secondary_xaxisund sichtbar machen axes.Axes.secondary_yaxis. Diese Sekundärachse kann eine andere Skalierung als die Hauptachse haben, indem sowohl eine Vorwärts- als auch eine Umkehrfunktion in einem Tupel für das Schlüsselwortargument functions bereitgestellt wird:

import matplotlib.pyplot as plt
import numpy as np
import datetime
import matplotlib.dates as mdates
from matplotlib.ticker import AutoMinorLocator

fig, ax = plt.subplots(constrained_layout=True)
x = np.arange(0, 360, 1)
y = np.sin(2 * x * np.pi / 180)
ax.plot(x, y)
ax.set_xlabel('angle [degrees]')
ax.set_ylabel('signal')
ax.set_title('Sine wave')


def deg2rad(x):
    return x * np.pi / 180


def rad2deg(x):
    return x * 180 / np.pi


secax = ax.secondary_xaxis('top', functions=(deg2rad, rad2deg))
secax.set_xlabel('angle [rad]')
plt.show()

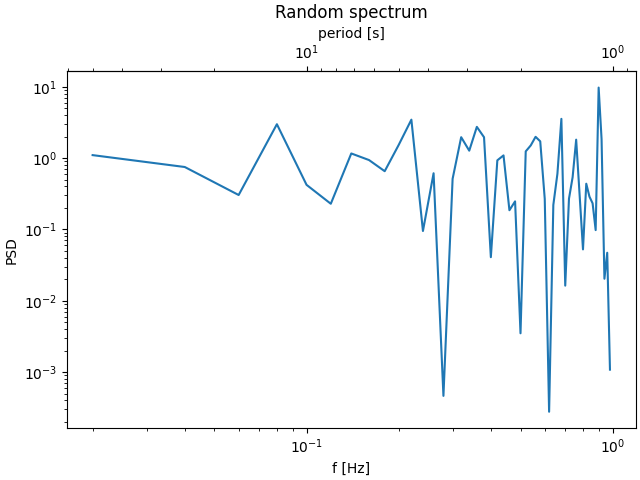
Hier ist der Fall der Umwandlung von Wellenzahl in Wellenlänge in einer Log-Log-Skala.

Notiz

In diesem Fall ist die xscale des Elternteils logarithmisch, also wird das Kind ebenfalls logarithmisch gemacht.

fig, ax = plt.subplots(constrained_layout=True)
x = np.arange(0.02, 1, 0.02)
np.random.seed(19680801)
y = np.random.randn(len(x)) ** 2
ax.loglog(x, y)
ax.set_xlabel('f [Hz]')
ax.set_ylabel('PSD')
ax.set_title('Random spectrum')


def one_over(x):
    """Vectorized 1/x, treating x==0 manually"""
    x = np.array(x).astype(float)
    near_zero = np.isclose(x, 0)
    x[near_zero] = np.inf
    x[~near_zero] = 1 / x[~near_zero]
    return x


# the function "1/x" is its own inverse
inverse = one_over


secax = ax.secondary_xaxis('top', functions=(one_over, inverse))
secax.set_xlabel('period [s]')
plt.show()

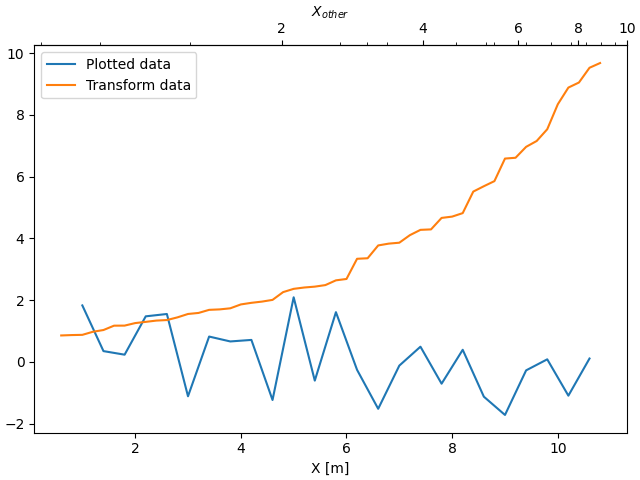
Manchmal möchten wir die Achsen in einer Ad-hoc-Transformation aus den Daten in Beziehung setzen und empirisch ableiten. In diesem Fall können wir die Vorwärts- und Rückwärtstransformationsfunktionen als lineare Interpolationen von einem Datensatz zum anderen festlegen.

Notiz

Um die Datenränder richtig handhaben zu können, müssen die Abbildungsfunktionen ( forwardund inversein diesem Beispiel) über die nominellen Plotgrenzen hinaus definiert werden.

Im speziellen Fall der linearen Numpy-Interpolation kann numpy.interpdiese Bedingung willkürlich erzwungen werden, indem optionale Schlüsselwortargumente left , right bereitgestellt werden, sodass Werte außerhalb des Datenbereichs deutlich außerhalb der Diagrammgrenzen abgebildet werden.

fig, ax = plt.subplots(constrained_layout=True)
xdata = np.arange(1, 11, 0.4)
ydata = np.random.randn(len(xdata))
ax.plot(xdata, ydata, label='Plotted data')

xold = np.arange(0, 11, 0.2)
# fake data set relating x coordinate to another data-derived coordinate.
# xnew must be monotonic, so we sort...
xnew = np.sort(10 * np.exp(-xold / 4) + np.random.randn(len(xold)) / 3)

ax.plot(xold[3:], xnew[3:], label='Transform data')
ax.set_xlabel('X [m]')
ax.legend()


def forward(x):
    return np.interp(x, xold, xnew)


def inverse(x):
    return np.interp(x, xnew, xold)


secax = ax.secondary_xaxis('top', functions=(forward, inverse))
secax.xaxis.set_minor_locator(AutoMinorLocator())
secax.set_xlabel('$X_{other}$')

plt.show()

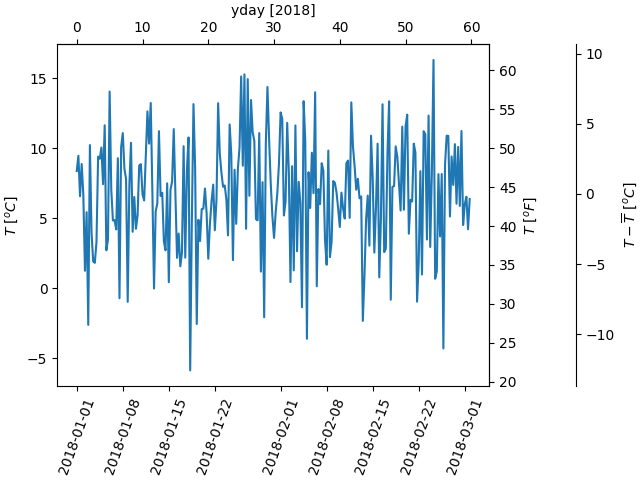
Ein letztes Beispiel übersetzt np.datetime64 in yearday auf der x-Achse und von Celsius in Fahrenheit auf der y-Achse. Beachten Sie, dass eine dritte y-Achse hinzugefügt wurde und dass sie mit einem Float für das Positionsargument platziert werden kann

dates = [datetime.datetime(2018, 1, 1) + datetime.timedelta(hours=k * 6)
         for k in range(240)]
temperature = np.random.randn(len(dates)) * 4 + 6.7
fig, ax = plt.subplots(constrained_layout=True)

ax.plot(dates, temperature)
ax.set_ylabel(r'$T\ [^oC]$')
plt.xticks(rotation=70)


def date2yday(x):
    """Convert matplotlib datenum to days since 2018-01-01."""
    y = x - mdates.date2num(datetime.datetime(2018, 1, 1))
    return y


def yday2date(x):
    """Return a matplotlib datenum for *x* days after 2018-01-01."""
    y = x + mdates.date2num(datetime.datetime(2018, 1, 1))
    return y


secax_x = ax.secondary_xaxis('top', functions=(date2yday, yday2date))
secax_x.set_xlabel('yday [2018]')


def celsius_to_fahrenheit(x):
    return x * 1.8 + 32


def fahrenheit_to_celsius(x):
    return (x - 32) / 1.8


secax_y = ax.secondary_yaxis(
    'right', functions=(celsius_to_fahrenheit, fahrenheit_to_celsius))
secax_y.set_ylabel(r'$T\ [^oF]$')


def celsius_to_anomaly(x):
    return (x - np.mean(temperature))


def anomaly_to_celsius(x):
    return (x + np.mean(temperature))


# use of a float for the position:
secax_y2 = ax.secondary_yaxis(
    1.2, functions=(celsius_to_anomaly, anomaly_to_celsius))
secax_y2.set_ylabel(r'$T - \overline{T}\ [^oC]$')


plt.show()

Verweise

In diesem Beispiel wird die Verwendung der folgenden Funktionen, Methoden, Klassen und Module gezeigt:

• matplotlib.axes.Axes.secondary_xaxis

• matplotlib.axes.Axes.secondary_yaxis