Konturdiagramm unregelmäßig verteilter Daten #

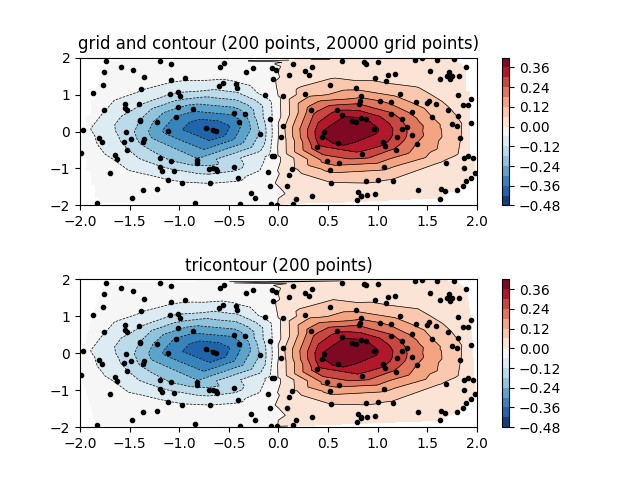
Vergleich eines Konturdiagramms von Daten mit unregelmäßigen Abständen, die auf einem regelmäßigen Gitter interpoliert sind, mit einem Trikonturdiagramm für ein unstrukturiertes dreieckiges Gitter.

Da die Daten auf einem regelmäßigen Raster leben contourund contourferwarten, erfordert das Zeichnen eines Konturdiagramms von Daten mit unregelmäßigen Abständen unterschiedliche Methoden. Die beiden Optionen sind:

Interpolieren Sie die Daten zuerst auf ein regelmäßiges Gitter. Dies kann mit integrierten Mitteln erfolgen, z. B. über LinearTriInterpolatoroder unter Verwendung externer Funktionalitäten, z. B. über scipy.interpolate.griddata. Zeichnen Sie dann die interpolierten Daten mit dem üblichen contour.
Verwenden Sie direkt tricontouroder tricontourf, das intern eine Triangulation durchführt.

Dieses Beispiel zeigt beide Methoden in Aktion.

import matplotlib.pyplot as plt
import matplotlib.tri as tri
import numpy as np

np.random.seed(19680801)
npts = 200
ngridx = 100
ngridy = 200
x = np.random.uniform(-2, 2, npts)
y = np.random.uniform(-2, 2, npts)
z = x * np.exp(-x**2 - y**2)

fig, (ax1, ax2) = plt.subplots(nrows=2)

# -----------------------
# Interpolation on a grid
# -----------------------
# A contour plot of irregularly spaced data coordinates
# via interpolation on a grid.

# Create grid values first.
xi = np.linspace(-2.1, 2.1, ngridx)
yi = np.linspace(-2.1, 2.1, ngridy)

# Linearly interpolate the data (x, y) on a grid defined by (xi, yi).
triang = tri.Triangulation(x, y)
interpolator = tri.LinearTriInterpolator(triang, z)
Xi, Yi = np.meshgrid(xi, yi)
zi = interpolator(Xi, Yi)

# Note that scipy.interpolate provides means to interpolate data on a grid
# as well. The following would be an alternative to the four lines above:
# from scipy.interpolate import griddata
# zi = griddata((x, y), z, (xi[None, :], yi[:, None]), method='linear')

ax1.contour(xi, yi, zi, levels=14, linewidths=0.5, colors='k')
cntr1 = ax1.contourf(xi, yi, zi, levels=14, cmap="RdBu_r")

fig.colorbar(cntr1, ax=ax1)
ax1.plot(x, y, 'ko', ms=3)
ax1.set(xlim=(-2, 2), ylim=(-2, 2))
ax1.set_title('grid and contour (%d points, %d grid points)' %
              (npts, ngridx * ngridy))

# ----------
# Tricontour
# ----------
# Directly supply the unordered, irregularly spaced coordinates
# to tricontour.

ax2.tricontour(x, y, z, levels=14, linewidths=0.5, colors='k')
cntr2 = ax2.tricontourf(x, y, z, levels=14, cmap="RdBu_r")

fig.colorbar(cntr2, ax=ax2)
ax2.plot(x, y, 'ko', ms=3)
ax2.set(xlim=(-2, 2), ylim=(-2, 2))
ax2.set_title('tricontour (%d points)' % npts)

plt.subplots_adjust(hspace=0.5)
plt.show()

Raster und Kontur (200 Punkte, 20000 Rasterpunkte), Trikontur (200 Punkte)

Verweise

In diesem Beispiel wird die Verwendung der folgenden Funktionen, Methoden, Klassen und Module gezeigt:

Galerie generiert von Sphinx-Gallery