Notiz
Klicken Sie hier , um den vollständigen Beispielcode herunterzuladen
Skaleninvarianter Winkel Label #
Dieses Beispiel zeigt, wie Sie eine skaleninvariante Winkelbeschriftung erstellen. Oft ist es sinnvoll, Winkel zwischen Linien oder innerhalb von Formen mit einem Kreisbogen zu markieren. Während Matplotlib eine bereitstellt Arc, besteht ein inhärentes Problem bei der direkten Verwendung für solche Zwecke darin, dass ein Kreisbogen, der im Datenraum kreisförmig ist, nicht unbedingt kreisförmig im Anzeigeraum ist. Außerdem wird der Radius des Bogens oft am besten in einem Koordinatensystem definiert, das unabhängig von den tatsächlichen Datenkoordinaten ist - zumindest, wenn Sie in der Lage sein möchten, frei in Ihr Diagramm hineinzuzoomen, ohne dass die Anmerkung ins Unendliche wächst.
Dies erfordert eine Lösung, bei der der Mittelpunkt des Bogens im Datenraum definiert ist, sein Radius jedoch in einer physikalischen Einheit wie Punkten oder Pixeln oder als Verhältnis der Achsendimension. Die folgende AngleAnnotationKlasse bietet eine solche Lösung.
Das folgende Beispiel dient zwei Zwecken:
Es bietet eine gebrauchsfertige Lösung für das Problem des einfachen Zeichnens von Winkeln in Diagrammen.
Es zeigt, wie man einen Matplotlib-Künstler in Unterklassen umwandelt, um seine Funktionalität zu verbessern, und gibt ein praktisches Beispiel für die Verwendung des Transformationssystems von Matplotlib .
Wenn Sie hauptsächlich an Ersterem interessiert sind, können Sie die folgende Klasse kopieren und zum Abschnitt Verwendung springen .
AngleAnnotation-Klasse #
Die wesentliche Idee hier ist, eine Unterklasse zu erstellen Arcund ihre Transformation auf die zu setzen IdentityTransform, wodurch die Parameter des Bogens im Pixelraum definiert werden. Dann überschreiben wir die ArcAttribute _center, theta1,
und von theta2, und machen sie zu Eigenschaften, indem wir sie mit internen Methoden koppeln, die bei jedem Zugriff auf das Attribut die entsprechenden Parameter berechnen und dadurch sicherstellen, dass der Bogen im Pixelraum mit den Eingabepunkten und der Größe synchronisiert bleibt. Jedes Mal, wenn die Zeichnungsmethode des Bogens beispielsweise sein
Attribut abfragt, erhält sie statt derselben Zahl das Ergebnis der Methode, die wir in der Unterklasse definiert haben. Diese Methode transformiert das Zentrum in Datenkoordinaten über die Axes-Transformation in Pixelwidthheight_centerget_center_in_pixelsax.transData. Die Größe und die Winkel werden auf ähnliche Weise berechnet, sodass der Bogen seine Form automatisch ändert, wenn zB interaktiv gezoomt oder geschwenkt wird.
Die Funktionalität dieser Klasse erlaubt es, den Bogen mit einem Text zu kommentieren. Dieser Text wird Annotationin einem Attribut gespeichert text. Da die Position und der Radius des Bogens erst beim Zeichnen definiert werden, müssen wir die Position des Textes entsprechend aktualisieren. Dazu wird die Methode von Arc's
neu implementiert , damit sie eine Aktualisierungsmethode für den Text aufruft.draw()
Der Bogen und der Text werden bei der Instanziierung zu den bereitgestellten Achsen hinzugefügt: Es ist daher nicht unbedingt erforderlich, einen Verweis darauf beizubehalten.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Arc
from matplotlib.transforms import IdentityTransform, TransformedBbox, Bbox
class AngleAnnotation(Arc):
"""
Draws an arc between two vectors which appears circular in display space.
"""
def __init__(self, xy, p1, p2, size=75, unit="points", ax=None,
text="", textposition="inside", text_kw=None, **kwargs):
"""
Parameters
----------
xy, p1, p2 : tuple or array of two floats
Center position and two points. Angle annotation is drawn between
the two vectors connecting *p1* and *p2* with *xy*, respectively.
Units are data coordinates.
size : float
Diameter of the angle annotation in units specified by *unit*.
unit : str
One of the following strings to specify the unit of *size*:
* "pixels": pixels
* "points": points, use points instead of pixels to not have a
dependence on the DPI
* "axes width", "axes height": relative units of Axes width, height
* "axes min", "axes max": minimum or maximum of relative Axes
width, height
ax : `matplotlib.axes.Axes`
The Axes to add the angle annotation to.
text : str
The text to mark the angle with.
textposition : {"inside", "outside", "edge"}
Whether to show the text in- or outside the arc. "edge" can be used
for custom positions anchored at the arc's edge.
text_kw : dict
Dictionary of arguments passed to the Annotation.
**kwargs
Further parameters are passed to `matplotlib.patches.Arc`. Use this
to specify, color, linewidth etc. of the arc.
"""
self.ax = ax or plt.gca()
self._xydata = xy # in data coordinates
self.vec1 = p1
self.vec2 = p2
self.size = size
self.unit = unit
self.textposition = textposition
super().__init__(self._xydata, size, size, angle=0.0,
theta1=self.theta1, theta2=self.theta2, **kwargs)
self.set_transform(IdentityTransform())
self.ax.add_patch(self)
self.kw = dict(ha="center", va="center",
xycoords=IdentityTransform(),
xytext=(0, 0), textcoords="offset points",
annotation_clip=True)
self.kw.update(text_kw or {})
self.text = ax.annotate(text, xy=self._center, **self.kw)
def get_size(self):
factor = 1.
if self.unit == "points":
factor = self.ax.figure.dpi / 72.
elif self.unit[:4] == "axes":
b = TransformedBbox(Bbox.unit(), self.ax.transAxes)
dic = {"max": max(b.width, b.height),
"min": min(b.width, b.height),
"width": b.width, "height": b.height}
factor = dic[self.unit[5:]]
return self.size * factor
def set_size(self, size):
self.size = size
def get_center_in_pixels(self):
"""return center in pixels"""
return self.ax.transData.transform(self._xydata)
def set_center(self, xy):
"""set center in data coordinates"""
self._xydata = xy
def get_theta(self, vec):
vec_in_pixels = self.ax.transData.transform(vec) - self._center
return np.rad2deg(np.arctan2(vec_in_pixels[1], vec_in_pixels[0]))
def get_theta1(self):
return self.get_theta(self.vec1)
def get_theta2(self):
return self.get_theta(self.vec2)
def set_theta(self, angle):
pass
# Redefine attributes of the Arc to always give values in pixel space
_center = property(get_center_in_pixels, set_center)
theta1 = property(get_theta1, set_theta)
theta2 = property(get_theta2, set_theta)
width = property(get_size, set_size)
height = property(get_size, set_size)
# The following two methods are needed to update the text position.
def draw(self, renderer):
self.update_text()
super().draw(renderer)
def update_text(self):
c = self._center
s = self.get_size()
angle_span = (self.theta2 - self.theta1) % 360
angle = np.deg2rad(self.theta1 + angle_span / 2)
r = s / 2
if self.textposition == "inside":
r = s / np.interp(angle_span, [60, 90, 135, 180],
[3.3, 3.5, 3.8, 4])
self.text.xy = c + r * np.array([np.cos(angle), np.sin(angle)])
if self.textposition == "outside":
def R90(a, r, w, h):
if a < np.arctan(h/2/(r+w/2)):
return np.sqrt((r+w/2)**2 + (np.tan(a)*(r+w/2))**2)
else:
c = np.sqrt((w/2)**2+(h/2)**2)
T = np.arcsin(c * np.cos(np.pi/2 - a + np.arcsin(h/2/c))/r)
xy = r * np.array([np.cos(a + T), np.sin(a + T)])
xy += np.array([w/2, h/2])
return np.sqrt(np.sum(xy**2))
def R(a, r, w, h):
aa = (a % (np.pi/4))*((a % (np.pi/2)) <= np.pi/4) + \
(np.pi/4 - (a % (np.pi/4)))*((a % (np.pi/2)) >= np.pi/4)
return R90(aa, r, *[w, h][::int(np.sign(np.cos(2*a)))])
bbox = self.text.get_window_extent()
X = R(angle, r, bbox.width, bbox.height)
trans = self.ax.figure.dpi_scale_trans.inverted()
offs = trans.transform(((X-s/2), 0))[0] * 72
self.text.set_position([offs*np.cos(angle), offs*np.sin(angle)])
Verwendung #
Erforderliche Argumente für AngleAnnotationsind der Mittelpunkt des Bogens, xy , und zwei Punkte, sodass sich der Bogen zwischen den beiden Vektoren erstreckt, die
p1 und p2 jeweils mit xy verbinden . Diese werden in Datenkoordinaten angegeben. Weitere Argumente sind die Größe des Bogens und seine Einheit . Zusätzlich kann ein
Text angegeben werden, der je nach Wert von textposition entweder innerhalb oder außerhalb des Bogens gezeichnet wird . Die Verwendung dieser Argumente wird unten gezeigt.
fig, ax = plt.subplots()
fig.canvas.draw() # Need to draw the figure to define renderer
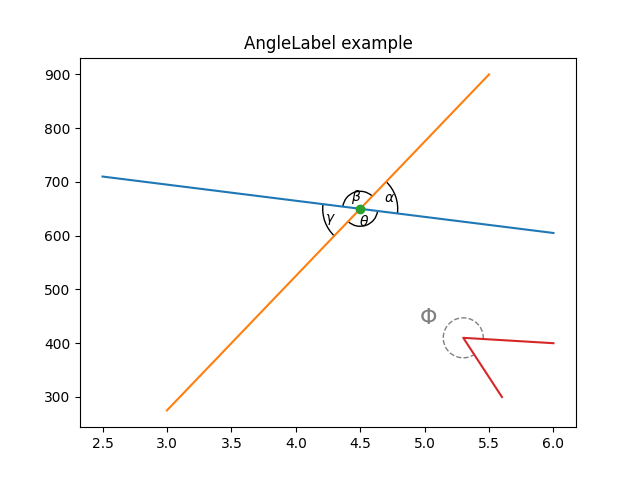
ax.set_title("AngleLabel example")
# Plot two crossing lines and label each angle between them with the above
# ``AngleAnnotation`` tool.
center = (4.5, 650)
p1 = [(2.5, 710), (6.0, 605)]
p2 = [(3.0, 275), (5.5, 900)]
line1, = ax.plot(*zip(*p1))
line2, = ax.plot(*zip(*p2))
point, = ax.plot(*center, marker="o")
am1 = AngleAnnotation(center, p1[1], p2[1], ax=ax, size=75, text=r"$\alpha$")
am2 = AngleAnnotation(center, p2[1], p1[0], ax=ax, size=35, text=r"$\beta$")
am3 = AngleAnnotation(center, p1[0], p2[0], ax=ax, size=75, text=r"$\gamma$")
am4 = AngleAnnotation(center, p2[0], p1[1], ax=ax, size=35, text=r"$\theta$")
# Showcase some styling options for the angle arc, as well as the text.
p = [(6.0, 400), (5.3, 410), (5.6, 300)]
ax.plot(*zip(*p))
am5 = AngleAnnotation(p[1], p[0], p[2], ax=ax, size=40, text=r"$\Phi$",
linestyle="--", color="gray", textposition="outside",
text_kw=dict(fontsize=16, color="gray"))
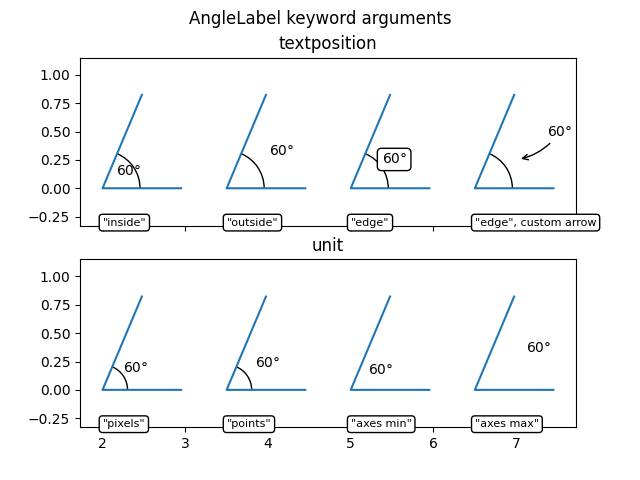
AngleLabelOptionen #
Die Schlüsselwortargumente textposition und unit können verwendet werden, um die Position der Textbeschriftung zu ändern, wie unten gezeigt:
# Helper function to draw angle easily.
def plot_angle(ax, pos, angle, length=0.95, acol="C0", **kwargs):
vec2 = np.array([np.cos(np.deg2rad(angle)), np.sin(np.deg2rad(angle))])
xy = np.c_[[length, 0], [0, 0], vec2*length].T + np.array(pos)
ax.plot(*xy.T, color=acol)
return AngleAnnotation(pos, xy[0], xy[2], ax=ax, **kwargs)
fig, (ax1, ax2) = plt.subplots(nrows=2, sharex=True)
fig.suptitle("AngleLabel keyword arguments")
fig.canvas.draw() # Need to draw the figure to define renderer
# Showcase different text positions.
ax1.margins(y=0.4)
ax1.set_title("textposition")
kw = dict(size=75, unit="points", text=r"$60°$")
am6 = plot_angle(ax1, (2.0, 0), 60, textposition="inside", **kw)
am7 = plot_angle(ax1, (3.5, 0), 60, textposition="outside", **kw)
am8 = plot_angle(ax1, (5.0, 0), 60, textposition="edge",
text_kw=dict(bbox=dict(boxstyle="round", fc="w")), **kw)
am9 = plot_angle(ax1, (6.5, 0), 60, textposition="edge",
text_kw=dict(xytext=(30, 20), arrowprops=dict(arrowstyle="->",
connectionstyle="arc3,rad=-0.2")), **kw)
for x, text in zip([2.0, 3.5, 5.0, 6.5], ['"inside"', '"outside"', '"edge"',
'"edge", custom arrow']):
ax1.annotate(text, xy=(x, 0), xycoords=ax1.get_xaxis_transform(),
bbox=dict(boxstyle="round", fc="w"), ha="left", fontsize=8,
annotation_clip=True)
# Showcase different size units. The effect of this can best be observed
# by interactively changing the figure size
ax2.margins(y=0.4)
ax2.set_title("unit")
kw = dict(text=r"$60°$", textposition="outside")
am10 = plot_angle(ax2, (2.0, 0), 60, size=50, unit="pixels", **kw)
am11 = plot_angle(ax2, (3.5, 0), 60, size=50, unit="points", **kw)
am12 = plot_angle(ax2, (5.0, 0), 60, size=0.25, unit="axes min", **kw)
am13 = plot_angle(ax2, (6.5, 0), 60, size=0.25, unit="axes max", **kw)
for x, text in zip([2.0, 3.5, 5.0, 6.5], ['"pixels"', '"points"',
'"axes min"', '"axes max"']):
ax2.annotate(text, xy=(x, 0), xycoords=ax2.get_xaxis_transform(),
bbox=dict(boxstyle="round", fc="w"), ha="left", fontsize=8,
annotation_clip=True)
plt.show()
Verweise
In diesem Beispiel wird die Verwendung der folgenden Funktionen, Methoden, Klassen und Module gezeigt:
Gesamtlaufzeit des Skripts: ( 0 Minuten 1,034 Sekunden)